Sunday morning puzzle.
(well, evening, if you are on the other side of the world).
Start by getting six identical coins. Arrange them in the pattern “A” as shown in the picture. (An equilateral triangle).
The goal is to eventually land up with the pattern “B” – again, as shown in the picture. (A straight line).
Here are the rules…
1. You cannot lift a coin – merely slide from its current position to the new position.
2. You move one coin at a time.
3. When you move a coin, no other coin changes position.
4. IMPORTANT: When you move a coin to a new position, in that new position, it MUST touch TWO other coins at least.
Finally, this is not a trick question – nor is there any sleight of the hand involved.
I am sure there are many ways of doing it but the one I got needed me 7 moves. (Not sure if that is the shortest way though)
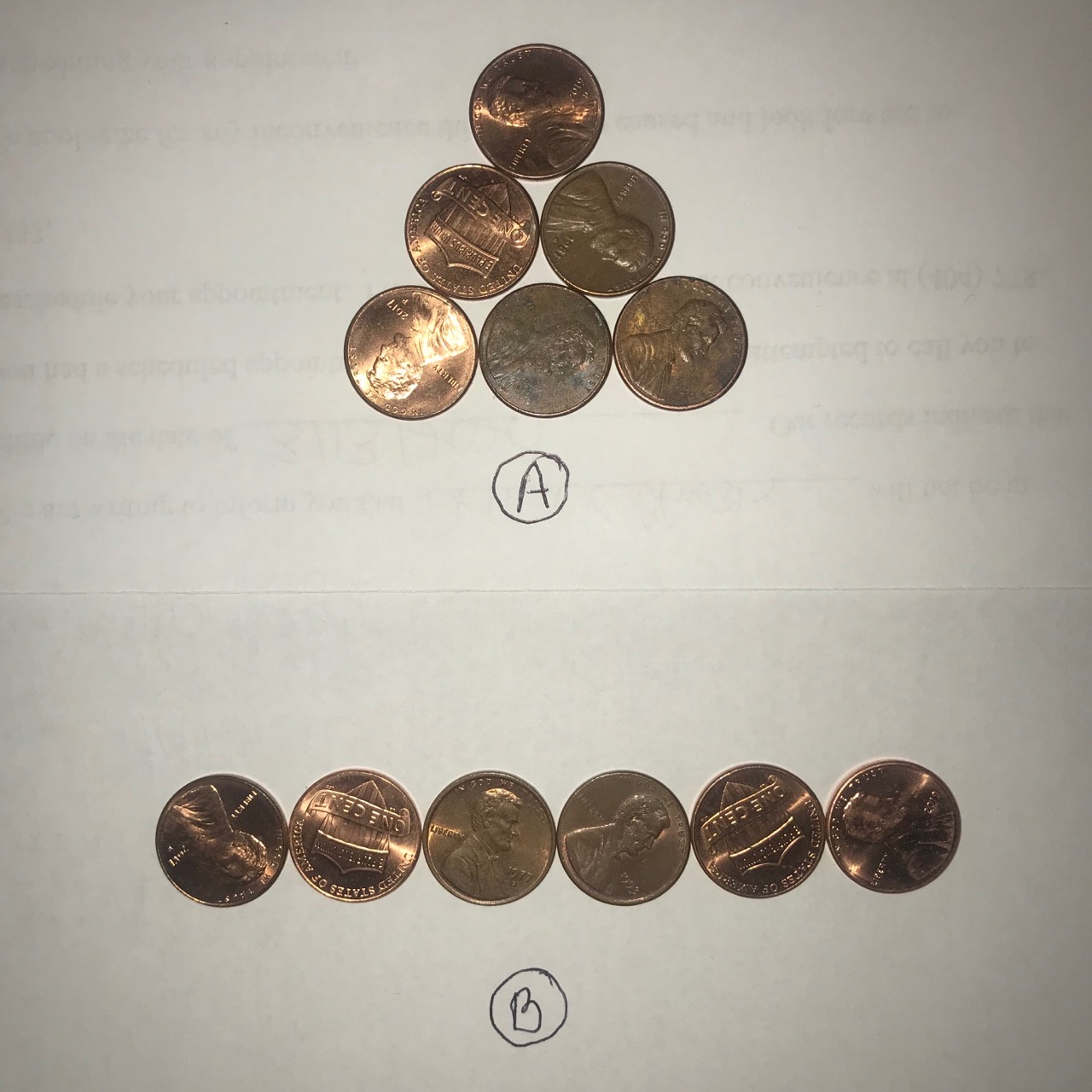







 The Dilbert cartoon today is really funny!
The Dilbert cartoon today is really funny!