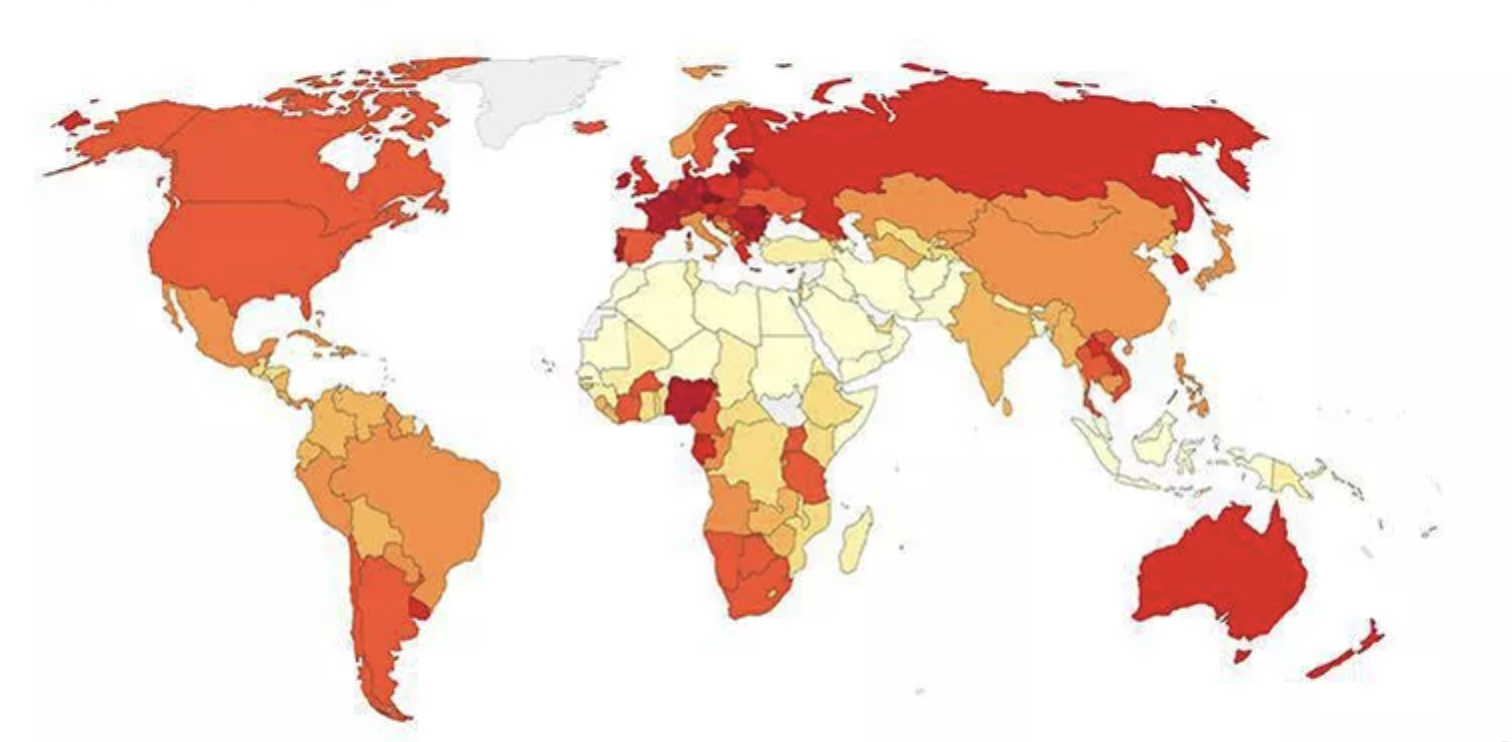
A quick number puzzle
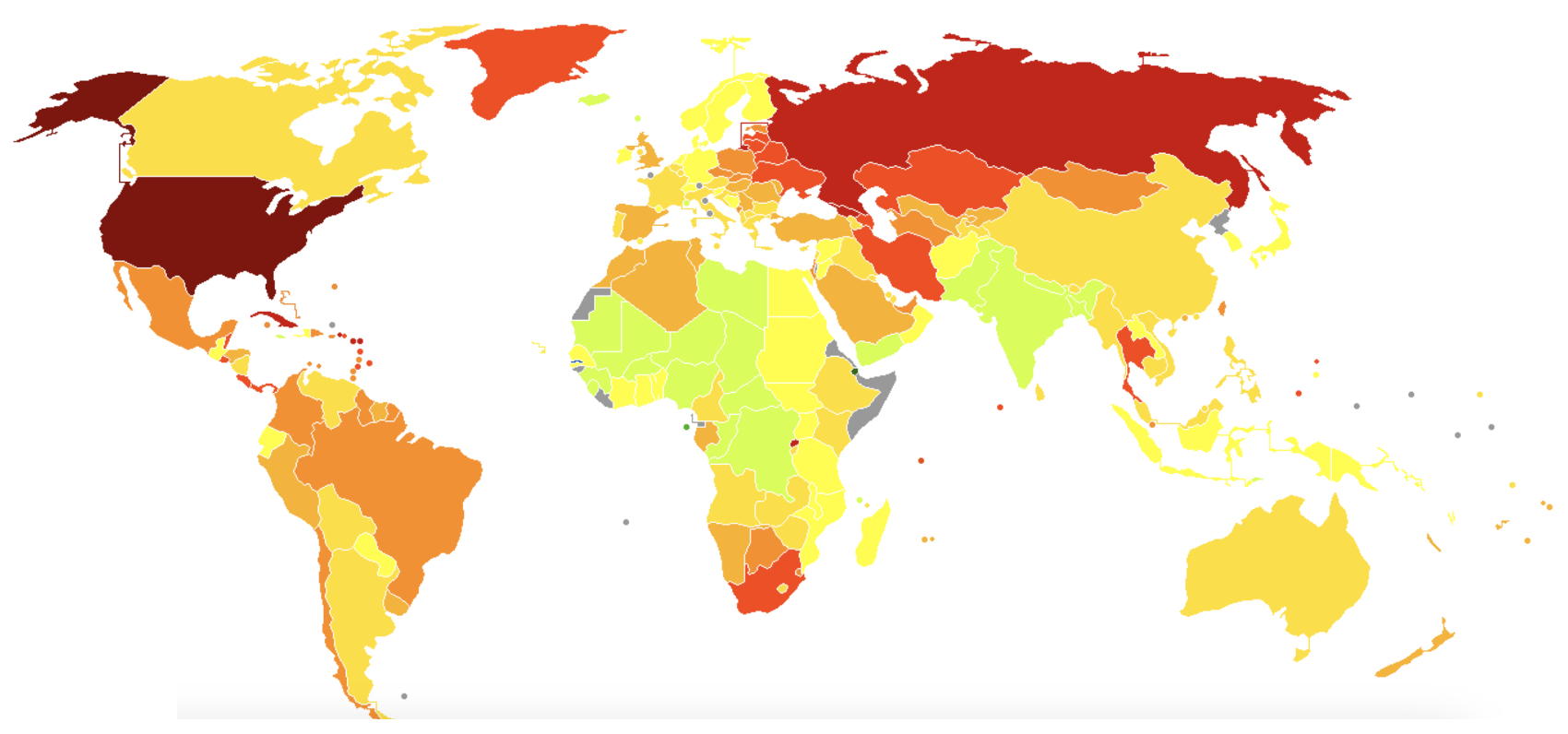
Sunday Map Quiz
What do you think this map represents? Darker means more. Post your answers in the Comments section
Answer can be found here.
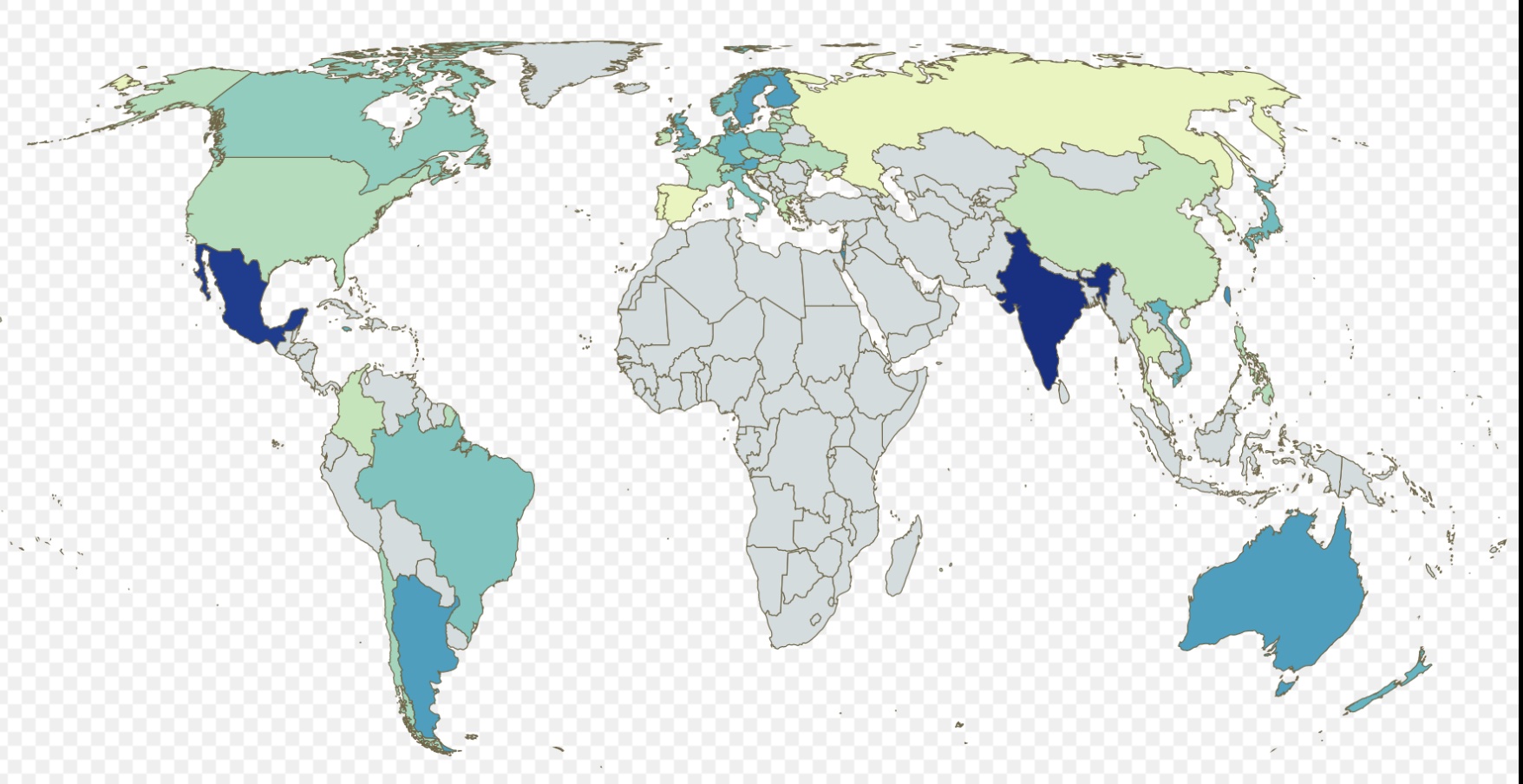
Puzzle: Numismatism – of a slightly different ilk
After putting all those currency notes under the table glass top, I had thought of sitting down and trying to learn all the modern currencies of the world. This has turned out to be much easier than remembering capital names and much much easier than flags (which I am still working on at a slow pace).
See how many of these you can answer. Since the definition of “country” can be a bit subjective, the scope of these questions are the 195 countries in the UN (193 members, 2 observers).
1. What is the currency used by the most number of countries? (US and Canada both use dollars – but they are different currencies with different paper bills – US Dollars and Canadian dollars)
2. If you found the above easy – try this: which is the second one?
3. A surprising number of countries have “dollars” in their currency names (e.g. Canadian dollars). Can you take a rough guess how many of them have it?
4. What would be your guess as the next common word in currency name? How many countries would you guess? I am talking of same currency name but differentiated by its region or country name. e.g. “rupee” is used by both Pakistan (Pakistani rupee) and India (Indian rupee)
5. Speaking of the rupee, and this surprised me – how many countries have the word “rupee” (or its close derivative) in its name?
6. There are many countries which have its own currency – but also use US Dollars (e.g. the Bahamas). But there are other countries than the US that use US Dollars as the only currency. Take a guess how many and who are they?
7. What would be your guess as the shortest currency name (without attaching the country name in it)? How many letters? How many of them would you guess are there?
8. This might be a hint to the previous question. How many countries have currencies that are only 4 letters?
You can find the answers here.

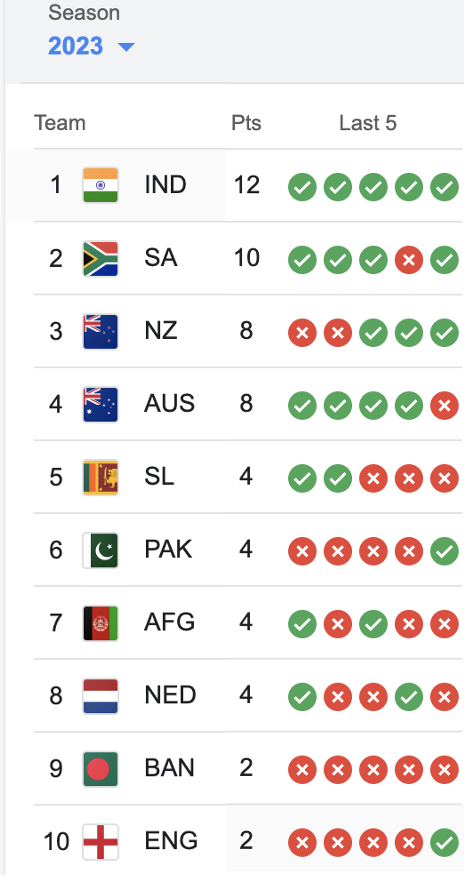
You do not need to know cricket to answer this quiz
Most of my friends in the USA may not be aware that World Cup Cricket is going on. There are 10 countries participating. (unlike our World Series Baseball where we just invite Canada in).
Each team will play the other 9 teams resulting in 45 games and then the top 4 go to semifinals and then of course, the final.
I was looking at where different countries stand today. This is how the chart looks. Country name, points and the result of the last five games, starting with the most recent.
Study that table carefully.
In any column, you would expect 5 wins and 5 losses, right? 10 teams playing each other – 5 winners, 5 losers. That is how you would expect every column to be. And that is how the third and fifth column indeed are. But the first, second and fourth column have 6 wins or losses and 4 wins or losses.
How is that possible?