Here is another problem to be solved
Now that we have solved the temperature problem in Chicago, here is another one from San Francisco.
[Errata: Looks like I have completely forgotten my physics – Sound is longitudinal and light is transversal – it is about which way the wave is moving and the particles in the wave are moving.
However, my original question remains – although I cannot remember the terms now – a ray of light goes straight but sound disperses in all directions – like the pool analogy. So, how does this work?]
Last week, I was in San Francisco and as his is wont, Matt Moore invited me to go for a walk with him by the waterfront and discuss business issues. While walking around Pier 15 enjoying some nice coffee, he showed me something. It is basically a set of two parabolic metals facing each other about 50 yards away. Each has a small stool to sit on. Matt asked me to go sit on one and he sat on another. As you can see in the picture.
Some of you might have guessed this, I could distinctly and loudly hear what he was saying. It felt like he was just six inches behind my head and he was talking to me from there with a slightly louder than usual voice of his.
For the next few minutes, I showed off my Physics to Matt by eloquently explaining how we were sitting in the focal points of the parabolas and how his voice was hitting his parabola, going then in a straight line to my parabola (geometric property of parabola if you remember) and then my parabola was putting all that on to its focal point which is where I was sitting. You would have seen the same in microwave towers, large telescopes etc. I do not know what Matt thought but I thought I did a good job.
Two days later, I realized what an idiot I was. I was telling Sharmila about it and then half way thru, I stopped cold. I realized that everything I said to Matt was correct but only for longitudinal waves – you know like microwaves, light etc. But sound is a transversal wave. It spreads out in concentric circles (like if you throw a stone in still pool). Those sound waves from Matt would have emanated as concentric circles and then after some of them hit the metal parabola, they would start out as more concentric circles from the point of incidence (where it hit the metal). Then where is the question of focus and all that in an ellipse?
But I experienced it myself.
How do you explain that?

How do you explain this?
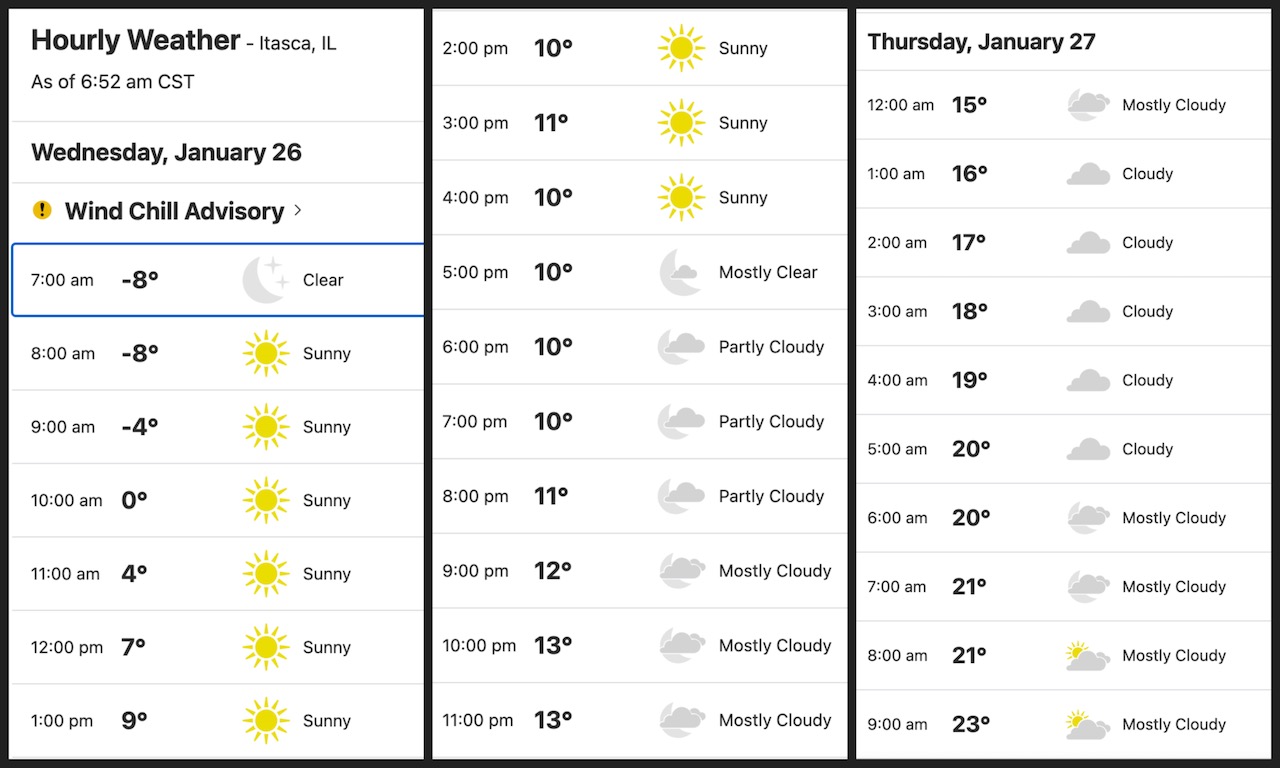
It is bone chilling -8F (-22C) right now here in Itasca. But it will slowly warm up as the sun comes up. That part I get. But look what happens after the sun sets. The temperatures keep rising thru the night. Of course, there is no sun around. Lake Michigan water cannot be that warm – after the last few cold days – to explain that.
How do you explain that?
Football score puzzle
In American football, any drive can end with the following points – 0 (ball turned over), 2 (safety), 3 (field goal), 6 (touchdown with failed point after or failed two pointer), 7 (touchdown and successful point after) or 8 (touchdown and successful 2 point conversion).
Assuming no team scores more than 50 points in a playoff match (there has to be a winner), what are the different legitimate combinations of scores that a match can possibly end with? (e.g. a game can end 14-2 but can never have a 27-1 score).

Answer to the marbles in Brownian motion puzzle…
The easiest way to think about this problem is not to think of number of marbles in each color but the differences in number between colors. Let’s say “a”, “b” and “c” are the pairwise differences in colors. Their values are 10, 10 and 20 to begin with.
Let’s see what happens whenever there is a “hit”.
If the marbles are of same colors, of course no change in count happens – so a, b and c remain the same.
If the marbles are of different colors – then those two colors go down by 1 each and the third color goes up by 2. Which means the pairwise differences either remain the same (the two colors that hit) or they change by 3 (one color goes down by 1 and the resulting color goes up by 2).
So, the first concept to realize is that a, b and c always change in steps of 0 or steps of 3. There are no other step changes they can have.
Now, let’s say what if the marbles actually did become all of one color. What as the step right before it? We would have had to have all marbles of the same final color excepting two – one each of the other two colors. Thus if finally everything is green, in the penultimate step, there has to be one red, one blue and rest green. The red hits the blue to become green.
Note that in that penultimate step, the pairwise difference between two colors (that have one marble left each) is 0. And that is the second concept to realize.
Now putting these two concepts together…
Well, we started with a, b and c being 10, 10 and 20. Going in steps of 0 and 3, can any of these numbers ever get to 0? No. Therefore it will never reach the penultimate step.
Which means the marbles will never be of the same color !!
Puzzle to get the weekend started
There is a large tray with red, blue and green marbles in it. In fact, there are 20 red marbles, 30 blue marbles and 40 green marbles. In that tray, the marbles are continuously moving around in Brownian (random) motion – often hitting each other.
If two marbles of same color hit each other, they just bounce off and continue. However, if two marbles of different color hit each other, then, both change to the third color and then bounce off and continue. All such hits are always between two marbles only. (no simultaneous three or more marbles hitting each other).
So a red and blue marble hitting each other will make both of them turn green and so on….
Is it ever possible for all the marbles in the tray to become of one color? If so, which color will it be?

Puzzle: Want to feel better after a Covid test?
This math puzzle about Covid will make your jaw drop (also make you feel better after getting a test)
First, please take all precautions again Covid. If you think you got exposed or have symptoms, get yourselves tested, quarantined and everything else CDC is asking us to do. Once you have done so, think about this puzzle…
The following puzzle – which is a very real one in Covid days – is an adaptation from a puzzle I had posted last year.
The end question I am going to ask you is this:
Q1. Your Covid test came positive. What is the probability that you really have the infection?
Q2. Your Covid test came negative. What is the probability that you really do not have the infection?
As Narayan had pointed out last year, most doctors do not get this. The fact that all tests have false positives and false negatives (they are not perfect) makes the real probability unintuitively high or low.
The real answers will knock your socks off.
Ok, let’s start this:
——
1. The COVID PCR test has a false positive of about 0.5% (*See Source). Which would mean in about 200 people without the virus, the test will make a mistake in one case and say he/she has the virus.
2. The test has a false negative of 10% (** See Source) This means of 10 people who actually have the virus, the test will miss out 1 of them.
3. Assume 2% of Americans at any point of time has the virus (*** See Source)
You went to get a PCR test done. Test showed positive. What is the real probability you have the virus? Hint: It is NOT 99.5%
Take the other case – the test showed negative. What is the real probability you do not have the virus? Hint: It is NOT 90%
Both the answers will make you feel much better.
That should be good enough reason why we should LOVE math! And at the risk of Tammi – the math teacher in my friend circle – slapping my wrist, I would say, you will love the chapter on Conditional Probability.
——
Sources:
* (in reality 0.2%-0.9% per https://www.icd10monitor.com/false-positives-in-pcr-tests…)
** the actual number can widely vary – as high as 67% – depending on when you got tested after exposure. The more time you give after exposure, the more the virus gets to establish itself and lesser the false negative number. https://www.acc.org/…/variation-in-false-negative-rate…
*** I took CDC’s 25% estimated US population had it https://www.cdc.gov/…/2019-ncov/cases-updates/burden.html over 11 months and took the average as 2%. (It will be slightly higher due to ramp ups)
Puzzles in a Singapore class
Yesterday, my blog reminded me of this incident from seven years back when my friend from Singapore – Jyotsna – had pointed out that puzzles from my blog were being discussed in the classes of Singapore. And she asked me to post more.
So, here goes a fairly interesting puzzle:
Imagine a pharmaceutical company in a race to find a cure for coronavirus. It has come up with 1000 chemical formulas as potential anti-virus vaccinations. Those chemical formulas are sitting as solutions in 1000 different beakers in their lab.
However, only 1 of them is effective. In fact, it is supereffective. Even a small trace of it injected in a rat’s body will extinguish the virus within 7 days. The other 999 are of no use. They also know that you can mix those chemical formulas up and the resultant concoction will retain all the properties of the original formulas. Put simply, in a combination of solutions, if you have even a little of the effective formula, the whole combination is supereffective. Else, any combination of those other 999 solutions is totally useless.
One catch is that the pharma company has exactly 7 days to win the race to a vaccination. Which means it gets only one time to inject rats with the various combinations of the chemicals and see what happens by the 7th day.
As if that was not enough, there is way too much demand for rats – apparently lots of pharma companies are trying to do experiments for the vaccination.
Finally, they have to find out the exact solution with the effective chemical formula – there is enough manufacturing capability to make only one of those solutions in a scaled manner.
What is the minimum number of rats the company has to procure to conclusively prove which one of the chemical formula is the ultimate solution against the virus? How would they do the experiment?
Really hard puzzle. Can you help me?
I have recently started doing Kenken puzzles (the 6×6 version). Last night, a question came to my mind and ever since I can neither solve the problem nor get it off my mind.
The usual Kenken is a 4×4 grid where you have to fill in every row and every column with the digits 1,2,3 and 4. One rule is that you have to have each one of those digits in every row and every column. (meaning therefore, no repeats in a row or column either – like Sudoku).
There are other rules for each individual Kenken problem. However, assume there is no other rule. You can fill in every row and every column with the digits 1,2,3 and 4 – with the only rule being you have to use each one of them once in every row and every column… how many such combinations are possible?
(I am attaching a picture here of an actual Kenken puzzle – but that

The girl does make me proud at times… (puzzle)
Usually, it is her sharp wit and acerbic comebacks. And at times it is her math capabilities. (It does take a nerd to recognize another).
Recently, my nephews had sent me a puzzle. Using 1, 1 and 1, you have to make 6. Similarly, using 2, 2 and 2… and then 3,3, and 3… and so on. You can use the normal mathematical operators – but no other digits. For example 2+2+2 = 6; They had given me till 10,10,10.
8 is a little tricky. It would be 8 – sqrt (sqrt (8+8)). Note that sqrt symbol does not use a digit.
During the walk last evening, Niki and tried 11,11,11 and then 12,12,12 and so. Once we reached 19,19,19… she said something that helped us find a completely generic way of getting to 6 given any number (repeated thrice).
For example, can you get 6 using 73, 73 and 73?
Note that you cannot split 73 into 7 and 3.
The mathematical operators allowed (any number of times) are plus, minus, multiply, divide, parentheses, square root, log and factorial. Give it a shot!

