26 May
2020
Another geometry puzzle
I sent this to my nephews since they have been sending me a few puzzles. See if you can beat them to it…
Orange circle inscribed inside an equilateral triangle inscribed inside a larger circle. Can you prove that the orange area is the same as the addition of the two purple areas?
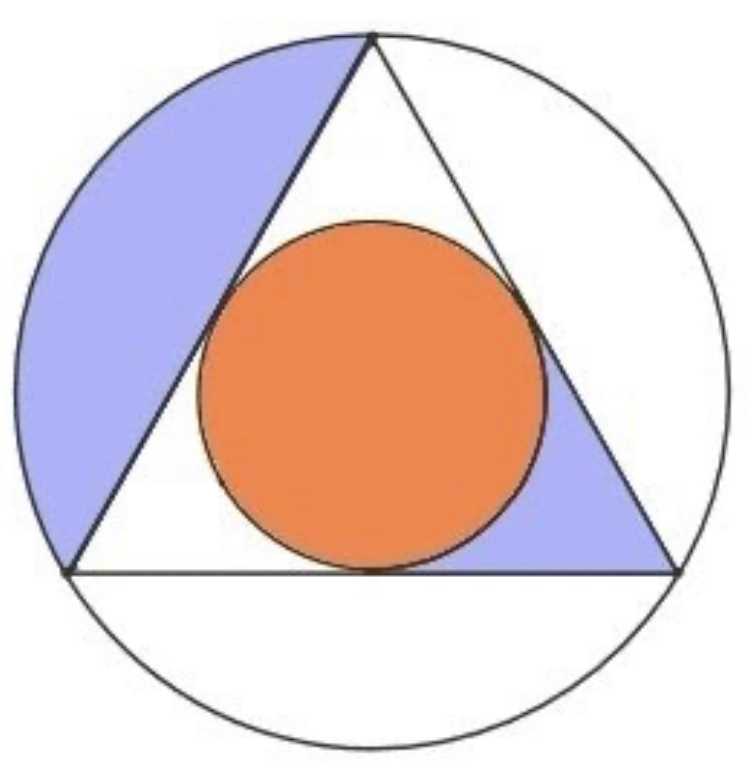
Rajibda consider the large circle area as 3x+3y+z, where each variable represents each unique shape. Z is the area of small circle. Now, the radius of big circle is 2 times that of small circle, as the centroid is located at 2/3 the distance from the vortex. Therefore area ratio between big and small circle is 4. Therefore 3x+3y+z = 4z. From this, x+y=z. The two purple areas add up to the orange area.
Somnath,
I am debating whether to accept the premise the centroid is located at 2/3 distance. It is a true statement though. I am inclined to accept that as something as “given” without having to prove.
On the other hand, there is another way of proving why the larger circle will be 4 times the smaller circle. Want to give it another shot?
Answer posted: https://www.rajibroy.com/?p=21441