This week’s puzzle
This week is another area problem. Take a rectangle ABCD (as shown here). Draw two lines from the adjacent vertices A and D to two random points E and F on the opposite side such that they intersect within the rectangle. See picture below. Nothing is drawn to scale. The area of the two triangles are 4 and 16. One of the quadrilaterals has an area of 10. What is the area of the other quadrilateral?
Again, this is geometry from elementary school with a twist to it.
Note that the original version of the problem that I had posted had the quadrilateral area as 1 instead of 10. Harmindar Matharu successfully proved that such a diagram is not possible. I should have been more careful while picking some values for those areas…
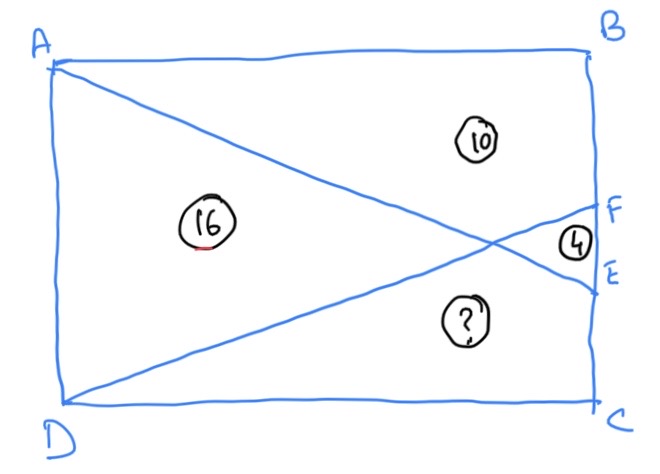
Area of the other quadrilateral = 16 + 4 – 1 = 19
The area of the other quadrilateral = 16 + 4 – 1 = 19
Harmindar, it will probably be far less than that. How did you get to the relationship that the sum of the triangles is the same as the sum of the quadrilaterals?
Move move the point F to B and move the point E to C, you get four triangles with equal areas. Move the points F and E to be at the same place, you get three triangles, one with side AD having area equal to the sum of the other two. This gave me the relationship that sum of two opposing triangles is same as the sum of the other two remaining triangles or the quadrilaterals.
Got it! I can see how in those two extreme cases, the logic holds. But there is no proof that it holds for other points too. In fact, it does not, actually.
(Also, I am not sure why your comments have to be approved everytime. I will look into it).
Have to callout Harmindar for his tenacity. Had a private exchange with him. He came very close.
The answer is posted here … https://www.rajibroy.com/?p=21144