One holiday puzzle
One of those letters for digits… with a twist.
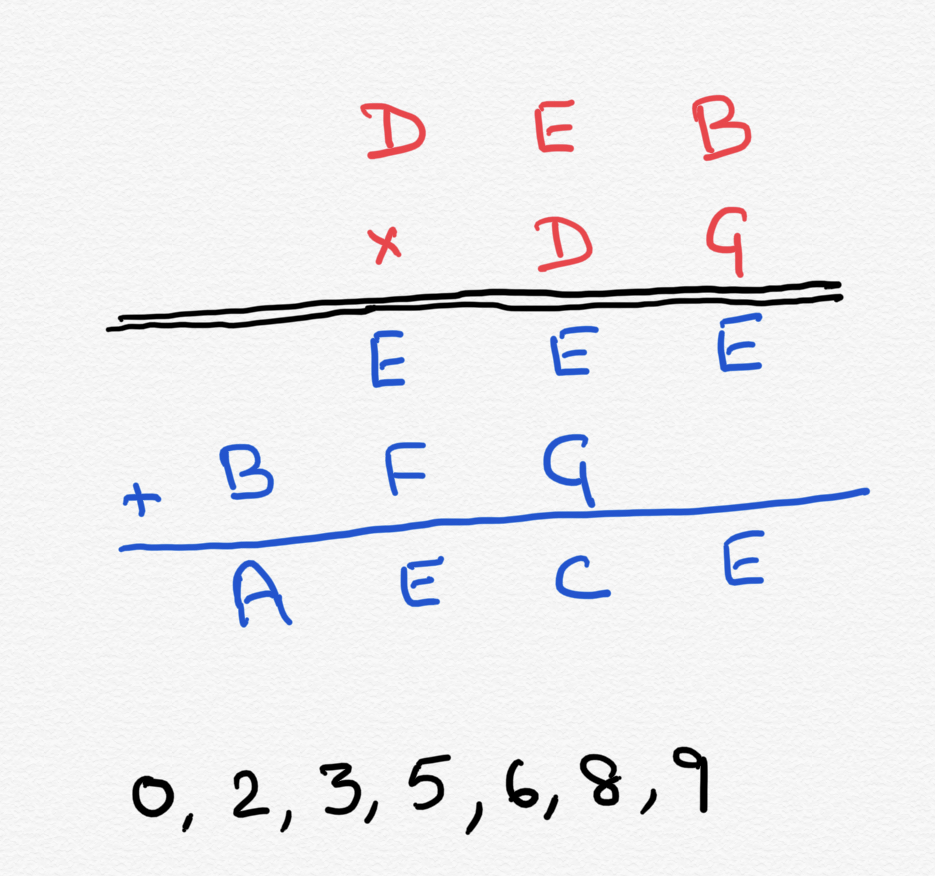
Look at the long multiplication below. As you see, a three digit number DEB is being multiplied by a two digit number DG to give a four digit number AECE. Each letter stands for a digit.
Here is the twist though: A letter above the black line (in red color) if also found below the black line (blue color) is not going to have the same value but will be off by one from each other. Of course, above the black line, any letter, if found twice will have the exact same value. Likewise below the black line. The twist comes only if the same letter comes both above and below the line.
As an example, the two D’s will have exactly the same value since they are both red. But the red G and the blue G are going to be off from each other by one since they have different colors. (If one is 6, the other can be 5 or 7).
The only digits used in this problem are 0,2,3,5,6,8 and 9.
Can you find out what the letters stand for above the black line and below the black line?
Red Letters:
D – 2
E – 9
B – 6
G – 3
Blue Letters:
E – 8
B – 5
F – 9
G – 2
A – 6
C – 0
Suresh, that is absolutely correct! Awesome!
Rajib, what helped me was the third line “EEE.” It had to be a multiple of 37.
Indeed, Suresh! I started with the F in the lower section. That gave me A and B below…
Didn’t get the logic, can anyone explain
Gurudutt,
Here is how I did it. I refer to rows from top to bottom and columns from left to right.
1. First look at Row 4. “F”. It has to be 9 or 0. “E” plus 0 can give “E” or “E” with 9 and a carry over of “1” from Column 3. It cannot be 0 because then in column 1, B has to be the same as A. So, F(blue) is definitely 9.
2. Then, B(blue) is 1 less than A(blue). Given the options of digits, they can be 2,3 or 5,6 (8,9 is not a possibility since 9 is already taken)
3. Let’s say B(blue) is 2 and A(blue) is 3. Then B(red) has to be 1 or 3. There is no 1. So, it has to be 3.
4. Now think of E(blue). It cannot be 0, 2,3 or 9 (all taken). SO, it can be 5, 6 or 8. Now, B(red) is 3. That means G(red) has to be 5. (only then E(blue) can be 5)). But if E(blue) is 5, which means row 3 is 555 and G(red) is 5, then row 1 has to be 111. So, that is rules out. E(blue) is not 5. It is either 6 or 8.
5. We know for a fact EEE (blue) is 666 or 888.
6. Go back to step 3 -> B(red) is 3 (Assuming B(Blue) is 2)
7. If EEE(blue) is 666 and B(red) is 3, then G(red) is 2. But if G(red) is 2, then DEB(red) has to be 333. That does not work.
8. If EEE(blue) is 888 and B(red) is 3, then G(red) is 6. But is G(red) is 6, then DEB(red) is 148. There is no 1 in the whole problem.
9. So, our original thesis of Step #3 is wrong
10. B(blue) has to be 5 and A(blue) as to be 6.
11. Which implies B(red) can be 4 or 6. Since 4 is not an option, B(red) is 6.
12. E(blue) can be 2,3 or 8 (since 5,6 and 9 are already taken by blue B,A and F). We can rule out 3 since B(red) is 6 and any G(red) multiplied by 6 will have to give an even number (blue)EEE.
13. Let’s say E(blue) is 2. So row 3 is 222. B(red) is 6. G(red) can be 2 or 7. 7 is not an option. so 2 is the only option.
14. If E(blue) is 2, then E(red) is 3 (1 is not an option). Row 1 looks like D36 and Row 2 looks like D2. You can see that this is not possible. The second “E(blue)” in row 3 is 3 times 2 plus carry over 1 which is 7 and not 2.
15. So, E(blue) has to be 8.
16. The rest flows from there.
17. third row is 888
18. first row is D96; which would imply D(blue) is 2. (other options don’t divide into 888)
19. so it is 296 multiplied by 23 giving first row as 888; second row as 592; third row as 6808
20. All the rules are obeyed.
Hope this helps..